恒达平台物理科學與工程學院王策/任捷教授AI for Science團隊在機器學習分類非厄米系統物態編織和紐結拓撲方向取得重要進展。在不需要任何先驗的數學物理知識的情況下，該團隊利用人工智能解決了非厄米物理和拓撲數學交叉領域的一個重要問題，利用n倍擴展倒易空間裏基於su(n)李代數表示的無監督流形學習，識別和分類了宇稱-時間對稱或對稱破缺下的非厄米物態編織和紐結拓撲，展示了其在非厄米拓撲物理，紐結、編織群方面的巨大潛力。研究成果以“Machine learning of knot topology in non-Hermitian band braid”為題🧎🏻‍➡️，發表在國際知名期刊Nature旗下《通訊-物理》（Communications Physics）。

紐結理論在自然科學中具有特殊意義，為理解各種物理系統的拓撲性質和相互作用提供了一種至關重要的數學語言9️⃣。例如🥸，從楊-巴克斯特方程解中導出的紐結不變量用於表征量子態的糾纏和拓撲性質。此外，紐結理論有助於探索拓撲問題，如拓撲絕緣體和拓撲超導體，它們表現出奇特的物相和受保護的性質。最近人們發現在倒易準動量空間中🗝，非厄米能帶結構的不同拓撲相可以用辮子編織群進行分類。而辮子編織群與紐結密切相關👷🏿‍♀️。將辮子編織的兩端相連而形成的閉合結構就能夠代表紐結。

然而🙋🏽，如何分類和識別非厄米能帶編織形成的辮子群和紐結拓撲態，仍然是個巨大的挑戰👨🏻‍🦼‍➡️。一方面，在數學領域🕶，科學家們曾提出多種用於識別紐結種類的拓撲不變量🖖🏿，比如亞歷山大多項式和瓊斯多項式等等🏄🏿👨🏼‍⚕️。這些基於代數方法的紐結不變量在計算上非常復雜📖。即便如此🧕🏽，僅依賴某個拓撲不變量難以保證實現紐結種類的完全分類🍝。另一方面，在非厄米能帶物理領域，最近掀起了一波研究小高潮，其周期性的能帶結構使得閉合辮子編織會產生豐富的紐結拓撲。非厄米哈密頓量的復特征值和特征向量會產生復雜的現象，如奇異點👋🏿、宇稱-時間對稱性破缺👩🏼‍🏫、非厄米趨膚效應、非阿貝爾編織等等🧝‍♂️。因此，非厄米系統中的拓撲相變可能更加復雜。如圖1所示🙎🏻，能帶結構可能受到額外對稱性的限製🙋🏽‍♀️，導致具有相同紐結拓撲的不同相👊🏿🫔。此外🙇🏻‍♂️，不同的手性也會導致不同的能帶辮子🙅🏽‍♂️。另外🤽🏻‍♀️🧑🏽‍🦳，物理系統裏🚆🧙🏽，編織的不僅僅是能帶（即特征值）🫂，還包括特征矢量（描述了物質狀態）。因此🫧，對非厄米物態編織和紐結拓撲的全面分類超出了純粹特征值數學問題的範疇。

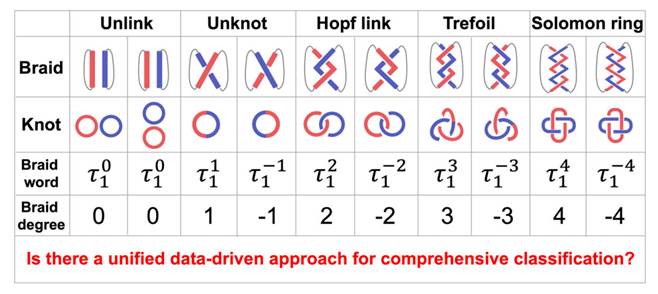
圖 1 一些例子，展示n=2非厄米帶中具有不同手性和拓撲相的辮子編織及對應的紐結

隨著人工智能的快速發展🙍‍♀️，監督神經網絡被應用於這些紐結拓撲識別。然而📱，監督學習的方法需要人們準備好已知紐結種類的大量先驗樣本，將需要消耗大量的計算資源，並且難以外延拓展去探索更復雜的紐結。人們迫切需要開發一種高效統一的無需監督的機器學習方案來識別和分類非厄米物理系統物態編織的豐富紐結拓撲相🧖🏻。

在最新發表的《通訊-物理》“Machine learning of knot topology in non-Hermitian band braid”這項工作中，科學家們采用了一種基於su(n)李代數的布洛赫矢量的擴散距離度量，即廣義Gell-Mann矩陣，來描述具有n條能帶的非厄米系統。這種度量可以結合哈密頓量復特征值和本征態的信息，對非厄米系中的物態辮子編織和紐結拓撲進行全面分類。值得註意的是，拓撲非平凡相中的非厄米能帶編織會導致自發對稱破缺的發生🧎‍➡️。因此，科學家們采用了n倍擴展的非厄米布裏淵區內的描述符🤳🏿，以確保每個模式始終保持2n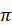的周期性。基於該描述符定義的擴散距離和擴散映射方法有效地區分了物態辮子和紐結的不同類型和手性。擴散映射是一種基於流形學習的非線性降維方法🧑🏻‍🦽‍➡️，能夠揭示數據集的內在微分流形結構。擴散映射的有效性依賴於樣本流形空間中的擴散過程與拓撲中的同倫之間的自然聯系。具體的，該工作以兩個模型為例（見圖2），一個n=2🐂，另一個n=3➖，實現了n條能帶的非厄米系統中紐結拓撲的精確分類👩🏿‍🔧，證明了上述描述符和機器學習方法的有效性💃🏽。

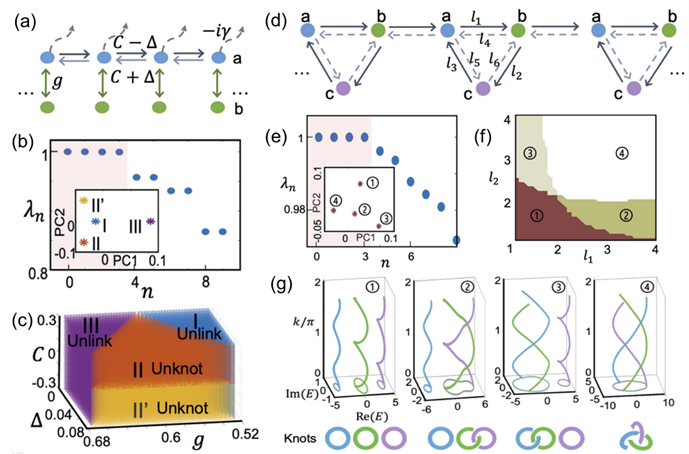
圖2 (a)-(c) 無監督學習對於n=2非厄米系統的分類結果；(d)-(g) 無監督學習對於n=3非厄米系統的分類結果   

恒达平台物理科學與工程學院博士生陳江芷和王子為論文共同第一作者🤹‍♂️。博士生譚宇濤也作出重要貢獻。王策助理教授與任捷教授為論文共同通訊作者。該項研究得到了國家自然科學基金、上海市原創探索項目、上海市優秀學術帶頭人、科技部重點研發和上海市特殊人工微結構材料與技術重點實驗室的資助🤸🏿。

論文鏈接：https://www.nature.com/articles/s42005-024-01710-w